Bienvenue sur notre site web, créé dans le cadre de notre TPE de 1ère S–SI. Celui-ci a pour problématique:
« En quoi la théorie du chaos, en utilisant des nouveaux outils comme l'informatique, permet-elle d'expliquer ou de modéliser des comportements complexes ou à priori aléatoires ? »
Ce sujet rentre dans la thématique « Avancées scientifiques et réalisations techniques ».
Sciences fondamentales et appliquées dans leurs rapports avec les réalisations techniques
Compréhension des phénomènes, modélisation, nouveau domaine de recherche scientifique
Ce TPE a été réalisé par Guilhèm Assael, Lucas Blaizot et Geert-Jan Huizing, élèves du lycée du Sacré-Cœur, durant les cours de SI au lycée Saint Eloi. Il a été encadré par M. Gardien et M. Halloum.
Le développement de la théorie du chaos commence durant la fin du XXe siècle. Celle-ci constitue une nouvelle approche par rapport à des problèmes scientifiques dans toutes les disciplines, aussi bien dans les mathématiques ou la physique que dans la médecine ou la biologie. En effet, la science « traditionnelle » s'appuie sur des notions comme le déterminisme 1
et cherche avant tout la prédictibilité. La théorie du chaos, pour sa part, a pour but de trouver un ordre dans le « chaos » apparent. Pour cela, elle s'appuie sur les notions de non-linéarité et d'auto-similarité et a pour outil expérimental de prédilection l'ordinateur.
La théorie du chaos, par son approche nouvelle, nous aide non seulement à mieux comprendre le monde qui nous entoure, mais apporte des applications concrètes et d'actualité dans des domaines aussi variés que la physique, la biologie, l'astronomie, la médecine, la communication radio et l'informatique.
Pour Kerry Emanuel, chercheur en météorologie au MIT 2, le chaos est la « Troisième révolution scientifique du XXème siècle, après la relativité et la mécanique quantique ».
Nous expliquerons ici en quoi la théorie du chaos, en s'appuyant sur des technologies relativement récentes comme l'ordinateur, permet d'expliquer des comportements complexes, ou à première vue aléatoires. Pour cela, nous définirons dans un premier temps de manière plus précise ce qu'est la théorie du chaos, ainsi que ses principes les plus importants. Dans un second temps, nous étudierons les applications possibles, certaines ayant déjà été réalisées, d'autres étant en cours de développement.
En 1997, George T. Yurkon, du département de physique de la Cleveland State University, explique :
« Lorsque l'on entend le mot chaos, ce qui vient à l'esprit est un lieu de désorganisation et de confusion totale. C'est la définition la plus courante du mot. Cependant, il y a eu une véritable explosion d'intérêt scientifique dans la théorie du chaos et la façon de l'exploiter. Si le terme ‘chaos’ n'impliquait que cette notion de désordre, il n'y aurait probablement aucun intérêt à étudier le phénomène.
Ici, le chaos signifie quelque chose qui semble aléatoire mais qui a en réalité une nature déterministe, ce qui signifie qu'elle est contrôlée de façon précise par des lois naturelles. Le désordre apparent est issu d'une sensibilité extrême aux conditions initiales, à l'image d'une balle de pinball semblant défier tout contrôle humain. »
Au début du XXème siècle déjà, le scientifique français Poincaré 3 avait remarqué cette notion de sensibilité aux conditions initiales :
« Une cause infime qui nous échappe détermine un effet considérable que nous ne pouvons pas ignorer […]. Même si les lois de la nature n'avaient plus de secret pour nous, […] nous pourrions seulement connaître la situation initiale de façon approximative. […] Il peut arriver que des petites différences dans les conditions initiales en produisent des très grandes dans le phénomène final. »
Voici à présent quelques définitions concernant des termes qui interviendront à de nombreuses reprises au cours de ce dossier.
Déterminisme
Le déterminisme est la théorie selon laquelle la succession des événements et des phénomènes est due au principe de causalité 4, ce lien pouvant parfois être décrit par une loi physico-mathématique qui fonde alors le caractère prédictif de ces derniers.
Il est lié à la prédictibilité qui stipule que chaque événement est prévisible selon des équations mathématiques.
Rationalisme Le rationalisme est la doctrine qui pose la raison discursive 5 comme seule source possible de toute connaissance réelle. Autrement dit, le rationalisme est constitué de toute doctrine qui attribue à la seule raison humaine la capacité de connaître et d'établir la vérité.
Non-linéarité On parle de non-linéarité lorsque l'entrée d'un système n'est pas proportionnelle à sa sortie, ou lorsqu'un événement a des effets imprévisibles à long terme.
Auto-similarité On parle d'auto-similarité quand on retrouve le motif de base à différentes échelles dans une sorte de mise en abîme. C'est le principe des fractales que nous étudierons par la suite (voir fig. 1.1).

Figure 1.1 – Exemple de structure auto-similaire
Espace des phases
Espace abstrait contenant sous forme géométrique une information concrète. Les variables qui sont à la base de la construction de cet espace sont des grandeurs réelles et à chaque point correspond une situation physique bien déterminée. Ainsi l’espace des phases du balancier d’une horloge est construit à partir des variables vitesse et angle par rapport à la verticale.
L’espace doit contenir toute l’information sur la dynamique du système étudié (voir fig. 1.2).

Figure 1.2 – Un espace des phases en trois dimensions (trois variables)
Edward Norton Lorenz 6
(1917 – 2008) est un scientifique américain largement considéré comme le père de la théorie du chaos.
Lorenz s'intéressait à la météorologie, qui n'était pas encore vraiment considérée comme une science par un grand nombre de personnes. A cette époque, on dépensait en effet beaucoup de ressources pour tenter d'établir des prévisions météorologiques très loin d'être précises.
Avec un modèle informatique basé sur trois variable seulement (simplifié jusqu'à le rendre presque ridicule par rapport à ceux développés par des instituts privés), Lorenz étudie la prévision du temps et obtient bientôt des résultats inédits.
Il démontre que les mouvements atmosphériques ne sont pas périodiques, et que des changements minimes dans les paramètres initiaux peuvent aboutir à des résultats totalement différents. C'est la sensibilité aux conditions initiales ou « effet papillon ».
Le terme « effet papillon » correspond à une image quelque peu poétique : le battement d'ailes d'un papillon peut provoquer une tornade à l'autre bout du monde. Mais l'origine première de ce terme vient en réalité de la forme de l'attracteur de Lorenz, qui peut être assimilée aux ailes d'un papillon (voir fig. 1.3).

Figure 1.3 – L'attracteur de Lorenz
L'attracteur de Lorenz est défini comme l'ensemble à long terme des trajectoires dans l'espace des phases du modèle créé par Lorenz.
Il conclut de sa découverte qu'il est impossible de réaliser une prévision météorologique précise à long terme. En effet, des incertitudes inévitables dans les données fournies aux modèles et de la quantité de paramètres à prendre en compte comme le vent, la température, le degré d'humidité rendent cela impossible.
De plus, il réalise qu'il suffit ici de trois variables seulement pour provoquer un comportement chaotique : l’introduction d’un nombre très limité de données peut induire une dynamique à la fois complexe et imprévisible.
Il met en évidence que la complexité peut être le propre d'un système. On pensait jusque-là qu’elle résultait d’apports accidentels dus à une multitude de causes.
En 1964, Lorenz formalise sa théorie du chaos. Il décrit comment, en jouant seulement sur quelques variables, un comportement chaotique peut être engendré dans un système en théorie très simple.
Manipulation
Pour illustrer l'effet papillon, Lorenz lui-même a construit un objet appelé le moulin de Lorenz. Le principe est simple :
On fixe sur une roue tournante un certain nombre de verres, répartis de manière égale sur celle-ci et percés au fond. Ces derniers sont alimentés par une source d’eau fixe et constante au sommet de la roue (voir fig. 1.4).
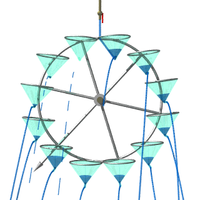
Figure 1.4 – Moulin de Lorenz
Ainsi, grâce à la force de l’eau, la roue tourne tantôt à gauche tantôt à droite, et il est impossible d’en prévoir le sens de rotation à long terme.
Il arrive aussi que le moulin se retrouve dans une PEI (position d’équilibre instable), moment temporaire d'immobilité où le moulin semble hésiter sur le direction à prendre.
Ce procédé simple illustre parfaitement les comportements chaotiques de la nature. En effet, si l'on choisit trois nombres pour décrire l'état du moulin, par exemple la vitesse angulaire et les coordonnées (x, y) du centre de gravité, et qu'on trace l'évolution de ces variables au cours du temps, on obtient l'attracteur de Lorenz.
Nous avons nous aussi construit un moulin de Lorenz, et nous avons réussi à obtenir un comportement identique à celui attendu.
Définition
Les fractales sont des schémas que la nature répète sans cesse. Les nuages, le corps humain, les montagnes, et les galaxies suivent des schémas fractals.
Une figure fractale ou fractale est une courbe ou surface de forme irrégulière qui se crée en suivant des règles déterministes ou aléatoires. Ce type de définition, appelée récursive implique une auto-similarité. Les fractales reprennent ainsi le principe fondateur de la théorie du chaos : l'ordre derrière le désordre apparent.
Le terme de « fractale » est un néologisme créé par Benoît Mandelbrot en 1974 à partir de la racine latine fractus, qui signifie « brisé, irrégulier ».
La géométrie fractale, par son irrégularité, se différencie de la géométrie classique ou euclidienne, qui utilise exclusivement des formes lisses.
Certains mathématiciens conservateurs ont donc encore du mal à accepter les fractales, mais de plus en plus reconnaissent cette nouvelle géométrie comme un véritable changement de paradigme (voir fig. 1.5).

Figure 1.5 – Exemple de fractale
Histoire
Le fondateur de la géométrie fractale est Benoît Mandelbrot 7
(1924 - 2010), dont nous avons cité le nom au paragraphe précédent. Il est l'auteur de Fractals : Form, Chance and Dimension 8. Il travaillait à l'époque chez IBM, qui recrutait beaucoup de scientifiques non conformistes.
Une de ses premières découvertes dans le domaine des fractales prend d'ailleurs place au sein de cette entreprise : on cherchait à résoudre un problème de parasites dans les lignes téléphoniques. Ce problème laissait ses collaborateurs perplexes, mais Mandelbrot découvrit que la répartition de ces parasites était la même à toutes les échelles. En d'autres termes, ils suivaient un schéma fractal. Peu à peu, Mandelbrot développe le principe de fractale, qui prend rapidement de l'ampleur dans la communauté scientifique.
S'en suivit une véritable explosion au niveau de la popularité des fractales. A l'image de l'effet papillon, les fractales sont l'un des seuls domaines scientifiques qui sont rentrés dans la culture populaire. Les couturiers par exemple, furent tout de suite charmés par ces entrelacements de couleur et ces motifs complexes, qui se fondaient parfaitement dans le contexte culturel des années ’80.
Exemples de fractales
Ensemble de Cantor :
L’ensemble de Cantor serait le premier exemple de fractale. Son inventeur, Georg Cantor, est un mathématicien allemand du XIXe siècle. Cet ensemble se construit par l’enlèvement du tiers central de chaque ligne. On obtient ainsi un ensemble de lignes de longueur nulle mais en nombre infini (voir fig. 1.6).

Figure 1.6 – L'ensemble de Cantor
Courbe de Koch :
La courbe de Koch est décrite par son créateur, Helge von Koch, comme un exemple de « courbe continue sans tangente, obtenue par une construction géométrique élémentaire ». Chaque segment est divisé en trois parties égales de longueur x et le segment central est transformé en deux segments de longueur x également. Cette opération se répète à l'infini. Par conséquent la courbe a une longueur infinie dans un espace fini (voir fig. 1.7).
Lorsque l'on accole trois courbes de Koch aux sommets d'un triangle équilatéral on obtient une figure à symétrie hexagonale dénommée « flocon de Koch » ou « île de Koch » (voir fig. 1.8).


Figure 1.7 – Deux étapes consécutives de la construction de la courbe de Koch


Figure 1.8 – Deux étapes consécutives de la construction du flocon de Koch
Ensembles de Julia et ensemble de Mandelbrot : Les ensembles de Julia appartiennent aux fractales les plus influentes et les plus célèbres. Un ensemble de Julia est défini par une suite : \[z_{n+1} = {z_n}^2 + c\]
Cette formule est répétée à l'infini, c et z0 étant des nombres complexes.
Pour une valeur donnée de c, l'ensemble de Julia correspondant est la frontière de l'ensemble des valeurs initiales z0 pour lesquelles la suite est bornée, l’ensemble de ces valeurs étant lui désigné comme l'ensemble de Julia rempli (voir fig. 1.9).

Figure 1.9 – Un ensemble de Julia
L’ensemble de Mandelbrot a été découvert par Gaston Julia 9 et Pierre Fatou avant la première guerre mondiale. Sa définition et son nom actuel sont l'œuvre de Adrien Douady, en hommage aux représentations qu'en a réalisées Mandelbrot alors qu'il travaillait chez IBM. L'ensemble de Mandelbrot M peut être défini comme l'ensemble des complexes c pour lesquels l'ensemble de Julia correspondant est connexe (voir fig. 1.10).

Figure 1.10 – L'ensemble de Mandelbrot
Nous avons réalisé les représentations ci-dessus d'un ensemble de Julia et de l'ensemble de Mandelbrot grâce au logiciel QFractalNow.
Triangle et tapis de Sierpiński : Le triangle de Sierpiński, du nom de son créateur Wacław Sierpiński, est un triangle équilatéral que l'on divise en quatre triangles plus petits. On enlève ensuite le triangle central et ainsi de suite pour tous les triangles. Le tapis de Sierpiński est une variante du triangle. Il s'agit cette fois d'un carré que l'on divise en 9 carrés plus petits et dont on enlève le carré central (voir fig 1.11).


Figure 1.11 – Triangle et tapis de Sierpiński
Principe de dimension fractale
On doit également à Mandelbrot la notion de dimension fractale. Dans son article « Combien mesure la côte de la Grande-Bretagne ? », il affirme qu'il est impossible de mesurer la longueur d'un côte. En effet, plus l'unité est petite, plus on peut saisir de détails, donc plus la côte sera longue.
Mais il affirme qu'il est possible d'en calculer la dimension fractale. Qu'est-ce donc une dimension fractale ?
On connaît les trois dimensions principales, la largeur, la hauteur et la profondeur, généralement notées x, y, et z.
Ainsi, une ligne a une dimension, une figure plane en possède deux, et un solide en a trois.
Si l'on double la taille d'une ligne, sa longueur est multipliée par 2 (21).
Si l'on double la taille d'une figure plane, son aire est multipliée par 4 (22).
Si l'on double la taille d'un solide, son volume est multiplié par 8 (23).
La dimension fractale est une dimension particulière, changeante selon les figures. Prenons pour exemple la courbe de Koch. Un agrandissement d’un facteur 3 de la courbe de Koch multiplie sa longueur par 4.
Sa dimension fractale est comprise entre 1 et 2 car 31 < 4 < 32.
On cherche donc un nombre d tel que 3d = 4. Nous avons besoin des logarithmes.
Le logarithme népérien d'un nombre x strictement positif vérifie la propriété : \[\ln(x^n) = n \cdot \ln(x)\]
Ainsi, \[\ln(3^d) = d \cdot \ln(3)\]
Comme 3d = 4 on a : \[d \cdot \ln(3) = \ln(4)\]
et ainsi : \[d = \dfrac{\ln(4)}{\ln(3)} \approx 1,262\]
On peut vérifier : \[3^{1,262} \approx 4\]
Cette dimension non entière est caractéristique des objets fractals. De la même manière, lorsque l’on agrandit le tapis de Sierpiński d’un facteur trois, on retrouve huit copies (les huit carrés autour du carré central) du tapis initial, ainsi sa surface est multipliée par 8. Sa dimension fractale d vérifie donc 3d = 8.
Par conséquent: \[d = \dfrac{\ln(8)}{\ln(3)} \approx 1,892\]
À cause des nombreux trous dans ce carrés, sa dimension se retrouve inférieure à 2.
Plus généralement, lorsqu’un objet fractal est dit « à similitude interne », comme les deux étudiées, c’est à dire qu’une partie de la fractale agrandie d’un facteur k donne la fractale entière constituée de N répliques de cette partie, sa dimension fractale est :
\[d = \dfrac{\ln(N)}{\ln(k)}\]
Revenons maintenant à la côte de la Grande-Bretagne. Celle-ci n'a pas de similitude interne.
L’idée est donc de recouvrir cet objet par une maille carrée de plus en plus fine et de ne compter que les carrés qui recouvrent l’objet (voir fig. 1.12).
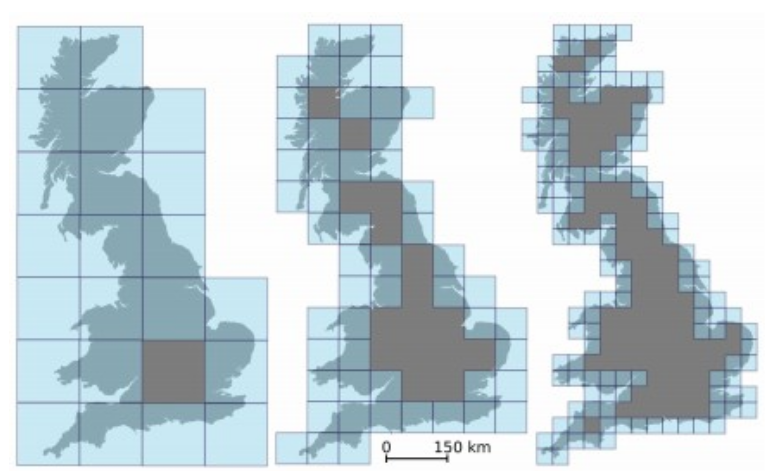
Figure 1.12 – La Grande-Bretagne recouverte par une maille carrée de plus en plus fine
On considère que l’objet est localement à similitude interne : si les carrés sont de côtés ε alors c’est en appliquant un agrandissement de 1/ε qu’on obtient le carré de longueur 1 et on peut estimer que chacun de ces petits carrés est une miniature d’un carré de côté 1. Si on note Nε le nombre de carrés nécessaires au recouvrement de la côte, sa dimension fractale sera pour ε assez petite :
\[d \approx \dfrac{\ln(N_\epsilon)}{\ln(\dfrac{1}{\epsilon})}\]
On compte le nombre Nε de carrés de côtés ε pour recouvrir la côte de la Grande Bretagne.
Pour ε assez petit, la dimension fractale est environ
\[\dfrac{\ln(N_\epsilon)}{\ln(\dfrac{1}{\epsilon})}\]
Plus formellement on obtiendra la dimension fractale en faisant tendre ε vers zéro. En notant dimF la dimension fractale d'un objet F on a donc :
\[dim_F = \lim\limits_{\epsilon \rightarrow 0} \dfrac{\ln(N_\epsilon)}{\ln(\dfrac{1}{\epsilon})}\]
L'avantage de cette méthode est de pouvoir se prêter à des calculs effectifs (par ordinateur) du comptage de carrés, donnant une valeur approchée de la dimension de n’importe quelle fractale dont on a une image.
L'attracteur étrange est une figure qui représente l'ensemble des trajectoires d'un système en proie à un mouvement chaotique.
On peut définir l'attracteur étrange comme une carte des états imprévisibles et chaotiques; il révèle un espace des phases vers lequel convergent des phénomènes chaotiques. On pourrait comparer cet espace des phases à une vallée dont toutes les eaux ruisselantes convergent vers un cours d'eau unique.
Les systèmes chaotiques peuvent être représentés géométriquement dans un espace dont le nombre de dimensions dépend du nombre de paramètres inhérents au système ; il peut donc y avoir plus de 3 dimensions, et l’on passe alors dans un espace abstrait.
L'état du système est alors représenté à chaque instant par un point dans l'espace des phases. On obtient une courbe qui correspond à la trajectoire de ce point. On constate alors que ce point est attiré vers une courbe limite, près de laquelle il repasse régulièrement.
Les mathématiciens appellent ces courbes des «attracteurs étranges», définitionnels de la théorie du chaos. Les attracteurs étranges ont par ailleurs une caractéristique bien particulière : tout comme les fractales, ils présentent une auto-similarité.
La figure 1.13 ci-dessous est un exemple d'attracteur étrange que nous avons générée grâce au logiciel Chaoscope, qui permet, par la modification de plusieurs paramètres, d'obtenir un rendu très complexe.

Figure 1.13 – Un attracteur étrange
Un jeu du chaos est un programme reposant sur un algorithme plus ou moins complexe, faisant intervenir des nombres aléatoires, pour générer une image point par point. L'image est donc générée de manière itérative, chaque point étant placé en fonction du point précédent et d'un nombre aléatoire. Un fractale apparaît rapidement. Nous avons réalisé deux types de jeu du chaos, implémentés chacun en Python (pour ordinateur) et en Java (à travers une application Android) 10.
Nous avons choisi la fougère de Barnsley et le triangle de Sierpiński, car selon nous, il s'agit des deux plus représentatifs du jeu du chaos.
La fougère de Barnsley À chaque itération, les deux nombres aléatoires (x et y) initiaux sont modifiés suivant la valeur du nombre aléatoire actuel (rand), testée par quelques conditions simples. Exemple en python:
if rand < 0.01:
x = 0.0
y = 0.16 * y
elif rand < 0.86:
x = (0.85 * x) + (0.04 * y)
y =(-0.04 * x) + (0.85 * y) + 1.6
elif rand < 0.93:
x = (0.2 * x) - (0.26 * y)
y = (0.23 * x) + (0.22 * y) + 1.6
else:
x = (-0.15 * x) + (0.28 * y)
y =(0.26 * x) + (0.24 * y) + 0.44
À partir du point aléatoire initial de coordonnées (x,y), une fougère est tout d'abord esquissée, puis précisée au fur et à mesure (voir fig. 1.14).
Sur une image d'assez bonne résolution, on retrouve l'aspect fractal d'une fougère.

Figure 1.14 – La fougère de Barnsley après 2000, 8000 et 20 000 itérations
Ceci pourrait être la manière dont la nature opère pour représenter les végétaux dans leur ADN ; en effet un faible nombre d'informations sur les opérations à effectuer à chaque étape de la croissance permettraient de décrire la structure du végétal, indépendamment de sa taille et de son âge.
Le triangle de Sierpiński
Cette fois, l'algorithme est extrêmement simple. En effet, on part de trois points a, b, c disposés en triangle, et d'un quatrième point p placé aléatoirement sur la zone. À chaque itération, un des sommets du triangle est sélectionné aléatoirement, puis un nouveau point p est placé à mi-chemin entre le sommet et le point p précédent.
Peu à peu, certaines zones du triangle se colorient, tandis que d'autres restent entièrement vierges (voir fig. 1.15).

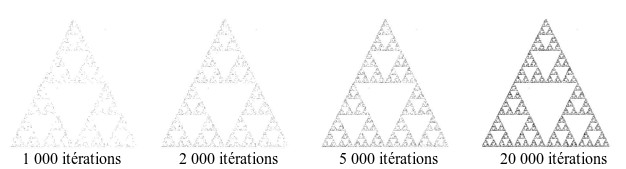
Figure 1.15 – Le triangle de Sierpiński
Il s'agit bien d'un motif fractal, le triangle principal se retrouve dans trois triangles deux fois plus petits, et ainsi de suite.
Le triangle de Sierpiński prouve qu'une suite d'opérations simples permet de générer une image complexe, et indescriptible au niveau géométrique puisqu'elle est infinie.
On peut se demander pour quelle raison un rythme qui a été régulier pendant une vie entière, soit plus de deux milliards de cycles ininterrompus, se détraque soudain pour mener à une crise cardiaque.
Nous nous devons tout de suite de nuancer cette dernière affirmation. En effet, le rythme cardiaque n'est pas réellement régulier. Il reste prévisible à grande échelle mais comporte des structures très complexes si l'on y regarde de plus près. Cette complexité dans le rythme cardiaque est en fait le signe d'une bonne santé: on peut observer chez les athlètes de haut niveau un motif très complexe, alors que des patients atteints d'une maladie cardiaque ont un motif simplifié.
Mais cette complexité est fragile. Le physicien et cardiologue du MIT Richard Cohen a réalisé une simulation informatique des rythmes cardiaques et a découvert qu'un faible dérèglement au sein du cœur peut mener à un état totalement chaotique.
Dans un cœur normal, des impulsions électriques se répandent dans les fibres musculaires qui contractent le ventricule. Une fois contractées, ces fibres musculaires sont insensibles aux signaux électriques. Les médecins qualifient cette période de réfractaire. Selon Richard Cohen, ce sont les variations de cette période réfractaire d’une zone du ventricule du cœur à une autre qui sont à l'origine d'une crise cardiaque.
Pour mettre cette théorie à l'épreuve, Cohen et son équipe ont fait varier les périodes réfractaires de leur modèle.
Ils ont découvert que les troubles cardiaques commençaient lorsqu’un groupe de fibres musculaires avait une période réfractaire plus longue que l’intervalle entre les battements. A cause de leur période réfractaire, ces fibres cardiaques asynchrones pouvaient être stimulées de manière à ne se contracter qu’un battement sur deux. En envoyant des impulsions électriques faibles de manière à déphaser le cœur, il était ainsi possible de l'amener à une crise cardiaque.
George Mines, de l’université McGill de Montréal, a estimé qu'il fallait réaliser l'expérience sur un être humain. En s’envoyant de très faibles chocs électriques, il s’est provoqué une crise cardiaque et est mort dans son laboratoire.
A l’université McGill toujours, le physiologiste Léon Glass a utilisé un groupe de cellules de cœur de poulet battant spontanément qu’il a stimulé avec un choc électrique régulier. Il a lui aussi réussi à conduire ces cellules à se comporter de manière totalement imprévisible.
Ces expériences suggèrent que la fibrillation cardiaque peut être provoquée par l’apparition de foyers anormaux secondaires à l’intérieur du corps, lesquels donnent des impulsions qui entrent en conflit avec le rythme propre au muscle cardiaque. L’interaction entre ces impulsions secondaires et le rythme principal met le cœur dans un état chaotique qui entraîne la fibrillation.
Cette découverte est d’une importance capitale et peut permettre d’améliorer les dispositifs de défibrillation.
Une méthode de détection du cancer du sein fondée sur les structures fractales a récemment été proposée. Traditionnellement, le diagnostic du cancer du sein est basé sur des évaluations morphologiques des cellules, telles que la taille, la forme ou la régularité. Mais la part de subjectivité de ces critères rend difficile un diagnostic objectif.
Andrew Einstein de la Columbia University et ses collaborateurs ont développé une méthode de diagnostic plus objective, qui exploite les propriétés fractales de ces aspects morphologiques des cellules du sein. L'irrégularité du noyau par exemple, qui est observée de manière subjective par le pathologiste, a pu être quantifiée à l'aide de deux dimensions fractales.
L'équipe d'Einstein a réalisé une étude sur un groupe de 41 femmes. Le diagnostic basé sur l'approche fractale s'est avéré correct dans 95% des cas. Cette étude ouvre la voie à des essais à plus grande échelle, qui pourraient sans doute révolutionner la détection de cancers.
Lorsque nos yeux suivent le mouvement d'un pendule, ils le suivent de manière fluide, selon une structure oscillatoire complexe. Chez les individus atteints de schizophrénie et même les personnes de leur entourage, ces mouvements oscillatoires sont perturbés et paraissent imprévisibles. Cette caractéristique relevée en 1908 est aujourd'hui l'un des rares moyens fiables de détecter les cas de schizophrénie. Bernardo Huberman, en 1986, réalise un modèle simplifié du mouvement oculaire et note la part de non-linéarité qui semble y appartenir. Souvent, le système se comporte de façon prévisible, mais d'autres fois il voit émerger un comportement chaotique. Il émet ainsi la supposition que la probabilité que quelqu'un soit atteint de schizophrénie est déterminée de façon génétique. Mieux comprendre les structures oscillatoires des yeux et déterminer si quelqu'un est génétiquement disposé à être schizophrène est d'une importance capitale pour l'avenir de la psychiatrie.
L'évolution d'une population est soumise à de nombreux facteurs, comme l'introduction d'un prédateur ou une augmentation des ressources alimentaires. Les biologistes ont ainsi commencé à créer des modèles mathématiques simples pour étudier l’évolution des populations.
Le modèle le plus simple est le schéma malthusien : la population est soumise à une croissance infinie, soumise à aucune limite.
Ainsi, si la population initiale est de 1000 et que le taux de croissance est de 10\% par an, la population sera de 1100 l’année suivante. Mais ce modèle n’est pas réaliste, car il ne tient pas compte des contraintes qui freinent la croissance : famines, maladies, …
Ils incorporèrent donc dans le modèle un facteur de freinage :
Cette équation est appelée équation logistique. Elle est aujourd'hui largement utilisée et permet des prédictions très réalistes. Contrairement à la première équation, celle-ci est chaotique et donne naissance à des structures très complexes.
L’équation logistique a été mise en pratique par des entomologistes pour calculer l’effet des insectes sur les vergers, par des généticiens pour mesurer la variation d’apparition de certains gênes au sein d’une population.
Les recherches de Brian J. Enquist, de l'université d'Arizona, ont montré que le comportement fractal d'un seul arbre permet de nous renseigner sur celui de toute une forêt. En effet, les embranchements suivent souvent un schéma fractal, c'est-à-dire qu'il est possible de déterminer le nombre de branches et leur surface en fonction de la taille d'un arbre, et d'appliquer cette méthode à l'ensemble des arbres d'une forêt. Ainsi, il a pu déterminer la consommation en CO2 de toute une forêt du Costa Rica. Cette méthode ouvre des possibilités énormes en ce qui concerne la préservation de l'environnement.
En 1988 à Boston, Nathan Cohen utilise les fractales pour révolutionner le domaine de la communication électronique.
Il est un radioamateur mais n'est pas autorisé à installer une antenne sur son immeuble. Après une conférence de Mandelbrot, l'idée lui vient de créer une antenne en forme de courbe de Koch.
Celle-ci se trouve être beaucoup plus efficace dans la mesure où elle permet de réduire la taille de l’antenne (et donc de lui éviter des problèmes avec le propriétaire) mais également d'augmenter le spectre de fréquences captées. Suite à cette découverte, Cohen prouve que pour avoir une efficacité optimale, une antenne doit obligatoirement avoir une structure auto-similaire. Aujourd'hui, les antennes fractales sont utilisées dans les téléphones, les ordinateurs et une grande variété d'objets électroniques.
Nathan Cohen est maintenant PDG de Fractal Antenna Systems, et fournit les gouvernements, armées et entreprises du monde entier avec des antennes de toutes tailles.
De nombreux chercheurs, dont Cohen, s’intéressent maintenant à l’invisibilité. En effet, en 2006, John Pendry, un physicien britannique membre de la Royal Society a eu l’idée de « tordre » les rayons lumineux autour d’un objet pour le rendre invisible. En effet, les rayons lumineux contournant l'objet, une personne positionnée en face de l'objet verrait la même chose que si l'objet n'y était pas. Depuis, les expériences se succèdent, avec des succès de plus en plus éclatants.
Pour dévier la lumière de sa trajectoire, le principe est d’utiliser un métamatériau, au motif très complexe et répétitif : autrement dit, un motif fractal. Les métamatériaux ne sont pas nouveaux en eux mêmes. On peut citer par exemple le traitement antireflet sur les verres de lunettes, largement utilisé. Mais ce matériau-ci est beaucoup plus complexe ; il est constitué d’une multitude de couches et de charges magnétiques faibles qui attirent ou repoussent le rayon lumineux.
En 2009, l’entreprise de Cohen a déposé le premier brevet pour « cape d’invisibilité »: https://www.google.com/patents/US8253639
Ils ont aussi été les premiers à en recouvrir un être humain : plus de la moitié des micro-ondes ont contourné l’obstacle (voir fig. 2.1).

Figure 2.1 – Le premier humain dans la « cape d’invisibilité »
D’autres expériences ont réussi à cacher un objet aux infrarouges. Cependant, il faudra encore un certain nombre d’années avant que cette technologie puisse s’étendre au spectre de la lumière visible, à la longueur d’onde beaucoup plus courte. La « cape d’invisibilité » ne rend donc pour l'instant les objets invisibles que dans le domaine de l'infrarouge. Mais cela suscite déjà beaucoup d'intérêt : pour les militaires par exemple, cette découverte permet de camoufler un char en voiture. Pour cela, ils détournent les rayons infrarouges, utilisés par les lunettes à vision nocturne.
En 1978, au siège de Boeing à Seattle, Loren Carpenter est chargé de la modélisation d'avions expérimentaux par ordinateur. Il veut ajouter les montagnes en arrière-plan, comme dans toutes les publicités de Boeing. Mais il n'a pas assez de puissance sur son ordinateur pour les générer. En utilisant la géométrie fractale ( ici en ajoutant des triangles de façon itérative ) il crée un résultat inédit et très réaliste. Il quittera plus tard Boeing pour Lucas Film où il réalisera entre autres la première planète entièrement modélisée numériquement pour Star Trek II.
Aujourd’hui, de nombreux programmes utilisés dans le monde des effets spéciaux utilisent les fractales.
Tout comme les phénomènes physiques, les sociétés humaines peuvent se révéler chaotiques.
Mark Michaels a déterminé sept lois fondamentales relatives aux comportements organisationnels et aux systèmes sociaux. Ces sept lois établissent que des systèmes simples peuvent devenir complexes et sont sensibles aux conditions initiales.
D'autres chercheurs comme le célèbre théoricien Erwin Schrödinger ont démontré certains aspects des lois de Michaels et établi des conditions à la présence de chaos dans les systèmes sociaux.
La théorie du chaos ne constitue pas une autre approche des sciences sociales mais s'inscrit dans la lignée de théories plus générales comme le structuro-fonctionnalisme 11 ou le systémisme 12.
L'équation logistique, vue dans un paragraphe précédent, peut également être appliquée à la manière dont se répand une rumeur ainsi qu’aux théories de l’apprentissage.
Les économistes se sont intéressés à la signification de la théorie du chaos et ses applications à l'économie. Il a été mis en évidence que l'étude de phénomènes économiques, d'apparence complexes et chaotiques, peut être facilitée par l'application de certains développements de la théorie du chaos.
Blake LeBaron s'est intéressé au problème de la prévision des dynamiques économiques, comme les fluctuations de la bourse. Ces recherches ont évidemment un attrait considérable pour beaucoup de personnes. Mais les résultats observés sont très variables. Dans certains cas, l'analyse des séries temporelles par les outils dérivés de la théorie du chaos permet de mettre en évidence une non-linéarité et/ou la présence d'un attracteur et donc de prévoir avec plus de précision l'évolution d'un système. Cependant, dans le domaine de la prévision, les diverses études n'ont pas apporté de preuves réellement convaincantes quant à la suprématie des outils du chaos sur les outils statistiques traditionnels.
Dans l'étude des conflits, il faut mentionner les travaux d'Alvin Saperstein. Il s'est intéressé aux relations entre nations et à la prévision de guerre et de paix. Il s'est également intéressé à l'instabilité de crise, c'est à dire l'avènement de petits points de divergence entre nations et leurs conséquences.
Cette modélisation permet une certaine prédictibilité à très court terme d'une guerre mais ne permettra jamais, naturellement, de déterminer à l'avance l'issue de celle-ci.
Nous avons pu constater les applications de la théorie du chaos sont nombreuses. Certaines sont déjà largement reconnues et utilisées, comme les antennes fractales. D'autres, comme la détection de cancer ou de schizophrénie, ont fait leurs preuves mais doivent encore être développées et ne sont que rarement utilisées. D'autres encore, comme l'économie, ne sont pas évidentes et nécessiteront sans doute un certain nombre d'années avant de présenter une réelle utilité.
Enfin, le fait que le chaos propose des opportunités incroyables pour le futur est indéniable et souligné par des inventions comme l'invisibilité par torsion des rayons lumineux.
Nous pouvons affirmer que la théorie du chaos, actuellement en pleine expansion, constitue un domaine de recherches très prometteur. En effet, elle permet d'expliquer un grand nombre de notions qui semblaient auparavant trop complexes, comme les fractales, ou des phénomènes obscurs tels les attracteurs étranges. Nombre d'innovations scientifiques et technologiques lui sont dues, notamment en médecine et en électronique.
Cependant, au-delà des applications déjà réalisées, la théorie du chaos a encore un avenir infiniment vaste, dont certaines facettes peuvent à ce jour sembler futuristes ou irréalisables, mais pourraient faire un jour partie de notre quotidien.
Afin de pouvoir présenter le jeu du chaos au jury plus simplement et pour montrer l'universalité du principe, nous avons décidé de transposer les programmes en python en application Android. Pour cela, nous avons réécrit le code en Java, en respectant des contraintes comme l'orientation de l'appareil et les différences entre les versions d'Android. L'application, une fois terminée, a été mise sur Google Play afin de pouvoir être téléchargée sur plusieurs appareils sans passer par l'ordinateur. Pour développer une application Android, il faut trois choses essentielles:
Le code source est disponible sur Github à l'adresse suivante:
https://github.com/Geji/android-chaos-game
L'interface est constituée de l'image générée et d'un "slider" pour faire varier le nombre d'itérations. L'application s'ouvre sur la fougère de Barnsley mais il est possible de basculer vers le triangle de Sierpiński.

Afin de partager notre expérience, nous avons créé ce site web, qui regroupe le dossier, le carnet de bord et les divers programmes informatiques réalisés au cours de l'année.
Pour mettre en page un site web, il est nécessaire de connaître le langage HTML (pour le « squelette » de la page), le CSS (pour choisir les couleurs, le style, la police d'écriture...) ainsi que le Javascript (pour les interactions avec l'utilisateur).
Nous avons utilisé le framework Bootstrap, qui fournit des outils et des styles pour accélérer le développement, et facilite l'adaptation de la page à toutes les tailles d'écran (téléphone, tablette, ...).
Le carnet de bord est présenté sous la forme d'une frise, générée avec Timeline.js.
Henri Poincaré est l'un des plus grands scientifiques de la fin du XIXe et du début du XXe. Il est mathématicien, mais aussi physicien et philosophe.
Poincaré naît le 29 avril 1854 à Nancy. Sa famille fait partie de l'élite intellectuelle de sa ville : son père est neurologue et professeur à la faculté de Médecine, et son cousin Raymond sera Président de la République de 1913 à 1920.
Poincaré suit des études brillantes : il remporte plusieurs fois le premier prix au Concours Général 13, et obtient son baccalauréat de sciences et de lettres. Admis à l'École Normale Supérieure et à Polytechnique, il choisit cette dernière.
Sorti ingénieur des Mines, Poincaré se consacre à la rédaction d'une thèse de doctorat en mathématiques qu'il présente le 1er octobre 1879. L'un des membres du jury, Gaston Darboux 14, y voit un « théorème intéressant », mais n'apprécie pas le travail de Poincaré à sa juste valeur.
Poincaré est nommé maître de conférences à la Sorbonne. Commence alors une intense activité scientifique : en trente ans, il publie une trentaine de volumes, et des centaines de notes, articles et mémoires. Ses travaux révolutionneront les mathématiques de l'époque, en approfondissant certaines notions, en en créant d'autres.
En 1889, Henri Poincaré devient réellement célèbre en recevant le prix du roi Oscar, roi de Norvège et de Suède passionné de mathématiques, pour un brillant mémoire sur le problème des trois corps 15.
Poincaré est aussi reconnu en tant que philosophe des sciences. Dans « La Science et l'hypothèse », publié en 1902, il affirme le rôle essentiel du principe de récurrence (omniprésent dans la théorie du chaos), et met en garde contre de nombreux artefacts de la physique de son époque, comme l'éther, le temps absolu et l'espace absolu. Le 28 juin 1909, il entre à l'Académie Française, privilège rare pour un scientifique.
En 1912 est publié son livre « Calcul des probabilités », où il explique que le hasard n'existe pas ; les comportements qui semblent aléatoires dépendent en fait de causes insignifiantes et invisibles :
« Une cause infime qui nous échappe détermine un effet considérable que nous ne pouvons pas ignorer […]. Même si les lois de la nature n'avaient plus de secret pour nous, […] nous pourrions seulement connaître la situation initiale de façon approximative. […] Il peut arriver que des petites différences dans les conditions initiales en produisent des très grandes dans le phénomène final. »
Poincaré avait donc introduit la notion d'effet papillon et de conditions initiales, qui sera exposée soixante ans plus tard par Edward Lorenz.
Henri Poincaré est décédé le 17 juillet 1912, après avoir laissé un travail mathématique, physique et philosophique immense.
Edward Norton Lorenz est un scientifique Américain largement considéré comme le père de la théorie du chaos. Ses contributions à cette dernière comprennent l'effet papillon et l'attracteur de Lorenz. Sa carrière s'est déroulée au MIT et il était membre de l'Académie des sciences américaine.
Lorenz naît le 23 mai 1917 à West-Hartford, Connecticut. Après des études brillantes de mathématiques au Dartmouth College (New Hampshire) et à l'Université d'Harvard (Massachusetts), il devient météorologiste pour l'armée de l'air américaine durant la seconde guerre mondiale.
En 1948, après la guerre, Lorenz réalise son doctorat de météorologie au MIT.
Ses recherches le mèneront, en 1964, à formaliser sa théorie du chaos. De 1977 à 1981, il est responsable du département de météorologie du MIT et en 1983, quatre ans avant sa retraite, il reçoit le prix Crafoord. En 1991, Lorenz reçoit également le prix Kyoto pour les sciences de la Terre et de la planète.
Il décède le 16 avril 2008 à Cambridge, Massachusetts.
Grâce à son modèle informatique simplifié, Edward Lorenz a étudié la prévision du temps. Il observe que des changements minimes dans les paramètres initiaux peuvent aboutir à des résultats totalement différents. C'est la sensibilité aux conditions initiales ou « effet papillon », que Poincaré avait pressenti avant lui mais pas formalisé.
Il conclut de sa découverte qu'il est impossible de réaliser une prévision météorologique précise à long terme. En effet, des incertitudes inévitables dans les données fournies aux modèles et de la quantité de paramètres à prendre en compte comme le vent, la température, le degré d'humidité rendent cela impossible.
De plus, il réalise qu'il suffit de trois variables seulement pour provoquer un comportement chaotique : l’introduction d’un nombre très limité de données peut induire une dynamique à la fois complexe et imprévisible.
Il met en évidence que la complexité peut être le propre d'un système. On pensait jusque-là qu’elle résultait d’apports accidentels dus à une multitude de causes.
Gaston Julia naît en Algérie, en 1893, dans un milieu populaire. Il n'en est pas moins un brillant élève. Il est rapidement repéré par un inspecteur de l'Instruction publique qui, après le baccalauréat, lui fait obtenir une bourse pour le lycée Janson de Sailly à Paris. Après un an, il est reçu premier aux concours d’entrée de Polytechnique et de l'ENS ; il choisira cette dernière. Il réalise ainsi 3 ans d’études supérieures scientifiques à la Faculté des sciences de l’université de Paris. En 1914, il obtient une agrégation de mathématiques.
Durant la guerre, Julia sera grièvement blessé au visage et devra porter toute sa vie un masque de cuir.
Après sa blessure, il présente son premier mémoire à l'Académie des sciences et obtient son doctorat ès sciences mathématiques en 1917.
Gaston Julia mènera une double carrière d'enseignant. Il devient répétiteur à l'École polytechnique pour le cours d'analyse de Jacques Hadamard le 1er décembre 1919. Il occupera ce poste pendant 17 ans. Il est ensuite nommé en 1937, à l'âge de 44 ans, professeur de géométrie, puis d'algèbre et géométrie, poste qu'il occupe jusqu'à sa retraite en 1964.
Parallèlement à son enseignement à l'École polytechnique, il occupe une série de postes prestigieux à l'ENS.
Julia décède en 1978, à Paris.
Ses travaux sur les fractales, même si Mandelbrot ne leur avait pas encore donné ce nom, ont largement contribué à l'état actuel d'avancement scientifique dans le domaine des fractales et de la théorie du chaos en général.
Benoît Mandelbrot était un mathématicien et informaticien, né à Varsovie le 20 novembre 1924. Il est l'inventeur de la théorie des fractales. D'origine juive, sa famille émigre à Paris en 1936 pour fuir la menace nazie. Mandelbrot y retrouve son oncle Szolem Mandelbrot, mathématicien : membre fondateur du groupe Bourbaki et professeur au Collège de France.
Après l'invasion allemande, la famille de Mandelbrot se réfugie à Brive-la-Gaillarde. Benoît poursuit alors ses études au lycée du Parc à Lyon, avant de rentrer en 1944 à l'École Polytechnique (lui aussi avait été accepté à l'ENS). Il y suit notamment les cours de Paul Lévy et de Gaston Julia. En 1949, après sa scolarité à l'École Polytechnique, Mandelbrot effectue un master d'aéronautique en Californie, puis revient en France pour effectuer une thèse soutenue dont le sujet est : "Contribution à la théorie mathématique des communications".
Après un postdoctorat à Princeton sous la direction de Von Neumann, puis un bref retour en France, Benoît Mandelbrot s'installe définitivement aux États-Unis en 1958 pour travailler au centre de recherche d'IBM. Il y trouve à la fois une grande liberté et l'accès aux moyens de calcul et de visualisation les plus performants de l'époque. Il s'intéresse alors à la transmission optimale des communications dans des milieux bruités, et ensuite aux objets mathématiques "étranges", présentant des similarités à des échelles différentes. C'est ainsi que lui vient son idée des fractales, présentée pour la première fois dans son livre Fractals : Form, Chance and Dimension, paru en 1975.
Le succès de sa théorie fut réel, autant dans la communauté scientifique, pour les nouveaux outils qu'elle apportait, qu'auprès du grand public, pour la dimension intriguante et esthétique des fractales. Lorsqu'il prend sa retraite d'IBM, en 1987, Mandelbrot devient professeur à l'Université de Yale. Il reçoit de nombreux honneurs, comme la médaille Franklin ou le prix Wolf. Il est décédé le 14 octobre 2010.
Veuillez visionner le carnet de bord sur un écran plus grand ou téléchargez le pdf
Vous pouvez ici télécharger notre dossier et notre carnet de bord en version pdf, ainsi que plusieurs programmes réalisés au cours de l'année.